CUDA 矩阵乘优化分析

通过Shared Memory加速矩阵乘(Double等类型)分析

64位数据矩阵乘优化访存分析
矩阵乘法的 CUDA 优化

64位数据矩阵乘优化访存分析 {#sector_1}

通过分析下面的代码，回答对应的两个问题(答案在文章结尾给出)。

🌰：

#define BLOCK_SIZE 16          // 定义块大小为16
#define MATRIX_DIM 256         // 定义矩阵维度为256

// 定义线程块和网格的尺寸
dim3 Block_dim(BLOCK_SIZE, BLOCK_SIZE);
dim3 Grid_dim(MATRIX_DIM / BLOCK_SIZE, MATRIX_DIM / BLOCK_SIZE);

// 启动核函数进行矩阵乘法运算
multiply <<< Grid_dim, Block_dim >>> (A_mat_d, B_mat_d, C_mat_d);

// 核函数，用于执行矩阵乘法
__global__ void multiply(const double * __restrict__ A_mat, const double * __restrict__ B_mat, double * __restrict__ C_mat)
{
    int i, j;
    double temp = 0;

    // 定义共享内存，用于存储块内的子矩阵
    __shared__ double A_shared[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ double B_shared[BLOCK_SIZE][BLOCK_SIZE];

    // 计算当前线程对应的全局行和列索引
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;

    // 循环遍历每个子矩阵块
    for (int tileNUM = 0; tileNUM < MATRIX_DIM / BLOCK_SIZE; tileNUM++)
    {
        // 计算子矩阵块内的索引
        j = tileNUM * BLOCK_SIZE + threadIdx.x;
        i = tileNUM * BLOCK_SIZE + threadIdx.y;

        // 将子矩阵块的数据加载到共享内存中
        A_shared[threadIdx.y][threadIdx.x] = A_mat[row * MATRIX_DIM + j];
        B_shared[threadIdx.y][threadIdx.x] = B_mat[i * MATRIX_DIM + col];
        __syncthreads();  // 同步，确保所有线程都完成加载

        // 进行子矩阵块的乘法运算
        for (int k = 0; k < BLOCK_SIZE; k++)
        {
            temp += A_shared[threadIdx.y][k] * B_shared[k][threadIdx.x];
        }
        __syncthreads();  // 再次同步，确保所有线程都完成计算
    }

    // 将计算结果写入全局内存
    C_mat[row * MATRIX_DIM + col] = temp;
}

根据代码提示分析描述，请说明

(1) 对于线程块block(1,1)，在tileNum是1上，代码26行执行完成的情况下，请说明，A_shared和B_shared分别保存了A_mat和B_mat的哪些数据，以及这些数据在Shared Memory中的内存布局。A_mat和B_mat中的数据以相对于起始位置的偏移表示，即类似代码中A_mat[row * MATRIX_DIM + j]的形式。
(2) 对于第30行代码temp += A_shared[threadIdx.y][k] * B_shared[k][threadIdx.x]; ，A_shared和B_shared访问shared memory是否导致bank conflicts，请分析说明。

关于上述问题的推荐阅读：

在做算子优化的时候（比如 GEMM），我们需要充分利用 shared memory 的 broadcast 机制，以及避免 bank conflicts 的出现。同时还会用 LDS.64 或 LDS.128 指令 (局部数据共享指令/ 汇编级)（也可以直接用 float2、float4）等一次访问 8 或 16 个 bytes。但在官方文档中，只介绍了每个 thread 访问 4 byte（即 32bit）时的 broadcast 机制和 bank conflict 情形。

对于每个线程访问一个数据的情况：

对于常规访存指令(32bits/4Bytes)的情况，每个word在 i % 32 bank上，每个 bank 在每个 cycle 的 bandwidth 为 32 bits(4 Bytes)，所以 shared memory 在每个 cycle 的 bandwidth 为 32 * 32 bits = 32 * 4 bytes = 128 bytes。
对于LSD.64(即每次取8Bytes数据)的访存指令，16个线程即可取得128 Bytes数据。这时CUDA 会默认将一个 warp 拆分为两个 half warp，每个 half warp 产生一次 memory transaction。即一共两次 transaction。

只有以下两个条件之一满足时，这两个 half warp 的访问才会合并成一次 memory transaction：

对于 Warp 内所有活跃的第 i 号线程，第 i xor 1 号线程不活跃或者访存地址和其一致；(i.e. T0==T1, T2==T3, T4==T5, T6==T7, T8 == T9, ......, T30 == T31, etc.)

对于 Warp 内所有活跃的第 i 号线程，第 i xor 2 号线程不活跃或者访存地址和其一致；(i.e. T0==T2, T1==T3, T4==T6, T5==T7 etc.)
（活跃是指有访存需求）

简单理解一下，当上面两种情况发生时，硬件就可以判断（具体是硬件还是编译器的功劳，我也不确定，先归给硬件吧），单个 half warp 内，最多需要 64 bytes 的数据，那么两个 half warp 就可以合并起来，通过一次 memory transaction，拿回 128 bytes 的数据。然后线程之间怎么分都可以（broadcast 机制）. 当然，这里的前提是没有产生 bank conflict。即没有从单个 bank 请求超过 1 个 word。

情形一

其实 bank conflict 是针对单次 memory transaction 而言的。如果单次 memory transaction 需要访问的 128 bytes 中有多个 word 属于同一个 bank，就产生了 bank conflict，从而需要拆分为多次 transaction。比如这里，第一次访问了 0 - 31 个 word，第二次访问了 32 - 63 个 word，每次 transaction 内部并没有 bank conflict。

这里也可以查看从矩阵转置看共享内存(CUDA)

对于128 位访存情况同理：

使用 LDS.128 指令（或者通过 float4、uint4 等类型）取数据时，每个 thread 请求 128 bits（即 16 bytes）数据，那么每 8 个 thread 就需要请求 128 bytes 的数据。
所以，CUDA 会默认把每个 half warp 进一步切分成两个 quarter warp，每个包含 8 个 thread。每个 quarter warp 产生一次 memory transaction。所以每个 warp 每次请求，默认会有 4 次 memory transaction。（没有 bank conflict 的情况下）。

类似 64 位宽的情况，当满足特定条件时，一个 half warp 内的两个 quarter warp 的访存请求会合并为 1 次 memory transaction。但是两个 half warp 不会再进一步合并了。

具体条件和 64 位宽一样：

对于 Warp 内所有活跃的第 i 号线程，第 i xor 1 号线程不活跃或者访存地址和其一致；(i.e. T0==T1, T2==T3, T4==T5, T6==T7, T8 == T9, ......, T30 == T31, etc.)

对于 Warp 内所有活跃的第 i 号线程，第 i xor 2 号线程不活跃或者访存地址和其一致；(i.e. T0==T2, T1==T3, T4==T6, T5==T7 etc.) (活跃是指有访存需求）

对于LDS.64, LDS.128数据的Bank Conflict更详细内容请见Reference_1.

Note

LDS.64：代表从局部数据共享中读取或写入 64 位（8 字节）的数据。
LDS.128：代表从局部数据共享中读取或写入 128 位（16 字节）的数据。
float2：表示包含两个 32 位浮点数的向量。例如，一个二维坐标 (x, y) 可以用 float2 来表示。
float4：表示包含四个 32 位浮点数的向量。例如，一个四维向量 (x, y, z, w) 或颜色值 (r, g, b, a) 可以用 float4 来表示。

矩阵乘法的 CUDA 优化 {#sector_2}

以单精度为例

矩阵乘

CPU 下的矩阵乘：

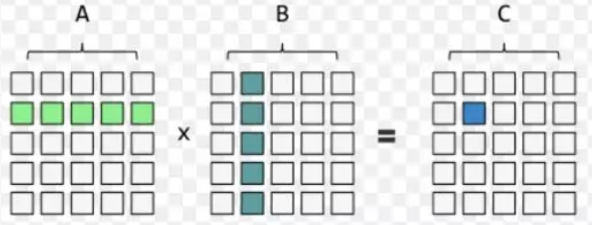
$A_{m \times k} \cdot B_{k \times n} = C_{m \times n}$

void matrixMulCpu(float* fpMatrixA, float* fpMatrixB, float* fpMatrixC,
int m, int n, int k)
{
    float sum = 0.0f;
    for(int i = 0; i < m; i++)
    {
        for(int j = 0; j < n; j++)
        {
            for(int l = 0; l < k; l++)
            {
                sum += fpMatrixA[i * k + l] * fpMatrixB[l * n + j];
            }
            fpMatrixC[i * n + j] = sum;
            sum = 0.0f;
        }
    }
}

上述 CPU 实现的代码中使用三层循环进行矩阵乘的计算，实际计算数达到了 $m \times n \times k$，时间复杂度为 $O(N^3)$.

GPU Native GEMM:

__global__ void matrixMul(const float *A, const float *B, float *C, 
                          int M, int N, int K) {
    int tx = blockIdx.x * blockDim.x + threadIdx.x;
    int ty = blockIdx.y * blockDim.y + threadIdx.y;
    if(ty < M && tx < N) {
        float c = 0;
        for(int i = 0; i < K; ++i){
            c += A[ty * K + i] * B[i * N + tx];
        }
        C[ty * N + tx] = c;
    }
}

在上述GPU Native代码中，矩阵A需要被重复加载 $k$ 次，矩阵B需要被重复加载 $m$ 次，在不考虑全局内存访存合并的情况下，矩阵中的每个元素都需要被重复加载 $m \times n \times k$次。加之全局内存访问延迟为几百 cycles，导致 GEMM 性能很低，计算/访存比极小。于是考虑利用共享内存低延迟、高带宽的特点，对矩阵乘进行分块处理。

共享内存优化矩阵乘

矩阵分块乘

// 矩阵分块乘
__global__ void matrixMultiplySharedKernel(float* matrixA, float* matrixB, float* matrixC, int rowsA, int colsB, int commonDim) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    float value = 0.0f;
    // 矩阵A和B的共享内存块
    __shared__ float tileA[TILE_SIZE][TILE_SIZE];
    __shared__ float tileB[TILE_SIZE][TILE_SIZE];
    // 矩阵分块的数量
    int numTiles = (commonDim + TILE_SIZE - 1) / TILE_SIZE;

    for(int t = 0; t < numTiles; t++) {
        // 将全局内存中的矩阵分块至共享内存中
        if(row < rowsA && t * TILE_SIZE + threadIdx.x < commonDim)
            tileA[threadIdx.y][threadIdx.x] = matrixA[row * commonDim + t * TILE_SIZE + threadIdx.x];
        else
            tileA[threadIdx.y][threadIdx.x] = 0.0f;

        if(t * TILE_SIZE + threadIdx.y < commonDim && col < colsB)
            tileB[threadIdx.y][threadIdx.x] = matrixB[(t * TILE_SIZE + threadIdx.y) * colsB + col];
        else
            tileB[threadIdx.y][threadIdx.x] = 0.0f;

        __syncthreads();
        // 每个线程计算block块中的乘积并累加
        for(int i = 0; i < TILE_SIZE; i++) {
            value += tileA[threadIdx.y][i] * tileB[i][threadIdx.x];
        }

        __syncthreads();
    }

    if(row < rowsA && col < colsB) {
        matrixC[row * colsB + col] = value;
    }
}

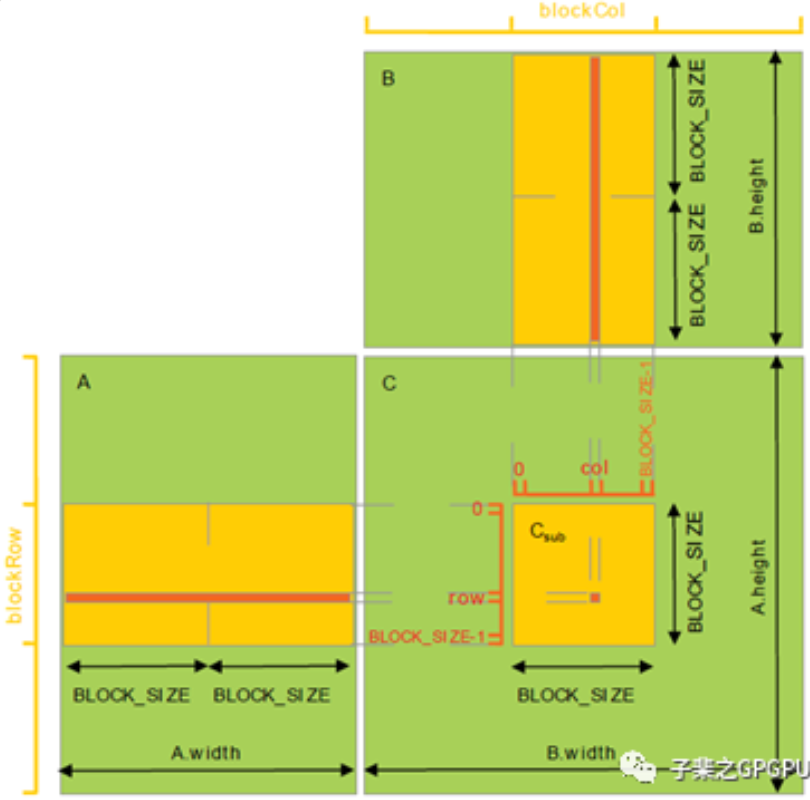
对矩阵乘进行分块处理，每个Block 计算一个子矩阵，通过对子矩阵向 numTiles 方向(矩阵A向行方向，矩阵B向列方向)进行迭代，计算矩阵C中每个元素的值。

寄存器优化矩阵乘(提高计算⬆️/访存比)

// 使用指令级并行（ILP）2来提高性能
__global__ void matrixMultiplySharedILPkernel(float* matrixA, float* matrixB,
float* matrixC, int rowsA, int colsB, int commonDim)
{
    int row = blockIdx.y * blockDim.y * 2 + threadIdx.y; // 每个线程块处理两个块
    int col = blockIdx.x * blockDim.x + threadIdx.x; // 列索引
    float value[2] = {0.0f}; // 用于存储两个结果值

    __shared__ float tileA[BLOCK_SIZE][BLOCK_SIZE]; // 共享内存中的子矩阵A
    __shared__ float tileB[BLOCK_SIZE][BLOCK_SIZE]; // 共享内存中的子矩阵B

    int numTiles = (commonDim + BLOCK_SIZE - 1) / BLOCK_SIZE; // 计算需要处理的子矩阵块数
    for(int t = 0; t < numTiles; t++)
    {
        // 从全局内存加载数据到共享内存
        tileA[threadIdx.y][threadIdx.x] = matrixA[row * commonDim + t * BLOCK_SIZE + threadIdx.x];
        tileA[threadIdx.y + 16][threadIdx.x] = matrixA[(row + 16) * commonDim + t * BLOCK_SIZE + threadIdx.x];

        tileB[threadIdx.y][threadIdx.x] = matrixB[(t * BLOCK_SIZE + threadIdx.y) * colsB + col];
        tileB[threadIdx.y + 16][threadIdx.x] = matrixB[(t * BLOCK_SIZE + threadIdx.y + 16) * colsB + col];

        __syncthreads(); // 确保所有线程都完成加载

        // 子矩阵乘法
        for(int j = 0; j < BLOCK_SIZE; j++)
        {
            value[0] += tileA[threadIdx.y][j] * tileB[j][threadIdx.x];
            value[1] += tileA[threadIdx.y + 16][j] * tileB[j][threadIdx.x];
        }

        __syncthreads(); // 确保所有线程都完成计算
    }

    // 将计算结果写入全局内存
    matrixC[row * colsB + col] = value[0];
    matrixC[(row + 16) * colsB + col] = value[1];
}

注意, kernel launch 时的 blocksize 需要变化为: blockSize.y = BLOCK_SIZE / 2。而 gridSize 不变.

事实上，上述程序对计算/访存比的提高并不明显，要显著提高程序运行效率可以采用向量化访存指令。

float c[4][4] = {{0}};
    float a_reg[4];
    float b_reg[4];
    for(int i = 0; i < K; i += TILE_K){
        __syncthreads();
        // transfer tile from global mem to shared mem
        load_gmem_tile_to_smem(A, i, smemA);
        load_gmem_tile_to_smem(B, i, smemB);
        __syncthreads();
    #pragma unroll
        for(int j = 0; j < TILE_K; ++j) {
            // load tile from shared mem to register 
            load_smem_tile_to_reg(smemA, j, a_reg);
            load_smem_tile_to_reg(smemB, j, b_reg);
            // compute matrix multiply accumulate 4x4
            mma4x4(a_reg, b_reg, c)；
        }
    }

上述伪代码程序中每次访存向量化达到提高计算/访存比的效果。

矩阵分块乘策略

考虑一个 block 计算 128x128 的分块，若每个线程计算 128 个结果，需要的 block size 为 128，单个线程需要 128 个寄存器储存计算结果，加上所需的 Gmem to Smem，Smem to Reg 等一些所需的寄存器，大概共需要至少 180 多个，计算 Occupany 可知此时的 Active Warp 数只有 8，Occupany 为 25%；若设置 block size 为 256，则每个线程仅需计算 64 个结果，调整寄存器和 Shared Memory 的使用量并观察 Occupany，可知若每个线程只使用 128 个寄存器，block 内的 Shared Memory 使用量限制在 32K，Active Warp 数可以达到 16，是一个更优的选择。

#define TILE_K 16
    __shared__ float4 smemA[2][TILE_K * 128 / 4];
    __shared__ float4 smemB[2][TILE_K * 128 / 4];
    float4 c[8][2] = {{make_float4(0.f, 0.f, 0.f, 0.f)}};
    float4 ldg_a_reg[2];
    float4 ldg_b_reg[2];
    float4 a_reg[2][2];
    float4 b_reg[2][2];

    // transfer first tile from global mem to shared mem
    load_gmem_tile_to_reg(A, 0, ldg_a_reg);
    load_gmem_tile_to_reg(B, 0, ldg_b_reg);

    store_reg_to_smem_tile_transpose(ldg_a_reg, 0, smemA[0]);
    store_reg_to_smem_tile(ldg_b_reg, 0, smemB[0]);
    __syncthreads();

    // load first tile from shared mem to register 
    load_smem_tile_to_reg(smemA[0], 0, a_reg[0]);
    load_smem_tile_to_reg(smemB[0], 0, b_reg[0]);

    int write_stage_idx = 1; //ping pong switch
    do {
        i += TILE_K;
        // load next tile from global mem
        load_gmem_tile_to_reg(A, i, ldg_a_reg);
        load_gmem_tile_to_reg(B, i, ldg_b_reg);

        int load_stage_idx = write_stage_idx ^ 1;

    #pragma unroll
        for(int j = 0; j < TILE_K - 1; ++j) {
            // load next tile from shared mem to register 
            load_smem_tile_to_reg(smemA[load_stage_idx], j + 1, a_reg[(j + 1) % 2]);
            load_smem_tile_to_reg(smemB[load_stage_idx], j + 1, b_reg[(j + 1) % 2]);
            // compute matrix multiply accumulate 8x8
            mma8x8(a_reg[j % 2], b_reg[j % 2], c)；
        }

        if(i < K) {
            // store next tile to shared mem
            store_reg_to_smem_tile_transpose(ldg_a_reg, 0, smemA[write_stage_idx]);
            store_reg_to_smem_tile(ldg_b_reg, 0, smemB[write_stage_idx]);
            // use double buffer, only need one sync
            __syncthreads();
            // switch
            write_stage_idx ^= 1;
        }

        // load first tile from shared mem to register of next iter
        load_smem_tile_to_reg(smemA[load_stage_idx ^ 1], 0, a_reg[0]);
        load_smem_tile_to_reg(smemB[load_stage_idx ^ 1], 0, b_reg[0]);
        // compute last tile mma 8x8
        mma8x8(a_reg[1], b_reg[1], c)；
    } while (i < K);

    store_c(c, C)

这段伪代码实现了一个矩阵乘法的CUDA核函数，其中使用了共享内存和寄存器来优化数据访问速度，采用双缓冲机制来提高计算效率。下面是对这段代码的逐步中文解析：

变量定义和初始化

宏定义：TILE_K 定义为16，这表示每个 tile 的大小为 16。
共享内存：
- smemA 和 smemB 是两个二维共享内存数组，每个数组有两个缓冲区，每个缓冲区大小为 TILE_K * 128 / 4。
寄存器：
- c 是用于存储结果的寄存器数组，初始化为全零。
- ldg_a_reg 和 ldg_b_reg 是用于从全局内存加载数据到寄存器的临时寄存器数组。
- a_reg 和 b_reg 是用于从共享内存加载数据到寄存器的临时寄存器数组。

初始化阶段

从全局内存加载第一块数据到寄存器：
- load_gmem_tile_to_reg 函数从全局内存中加载数据到 ldg_a_reg 和 ldg_b_reg。
将寄存器数据存储到共享内存：
- store_reg_to_smem_tile_transpose 将 ldg_a_reg 的数据转置后存储到共享内存 smemA[0] 中。
- store_reg_to_smem_tile 将 ldg_b_reg 的数据存储到共享内存 smemB[0] 中。
同步线程：
- __syncthreads() 用于确保所有线程都完成了对共享内存的写入。
从共享内存加载数据到寄存器：
- load_smem_tile_to_reg 将共享内存 smemA[0] 和 smemB[0] 中的数据加载到寄存器 a_reg[0] 和 b_reg[0]。

计算阶段

初始化双缓冲开关：write_stage_idx 设置为 1。
主计算循环：使用 do-while 循环来遍历整个 K 维度。
- 更新全局内存指针：i += TILE_K。
- 加载下一块数据到寄存器：从全局内存中加载下一块数据到 ldg_a_reg 和 ldg_b_reg。
计算循环：使用 #pragma unroll 展开内部循环，加速计算。
- 从共享内存加载下一块数据到寄存器：每次从共享内存加载下一行 tile 数据到寄存器 a_reg[(j + 1) % 2] 和 b_reg[(j + 1) % 2]。
- 矩阵乘法累积计算：调用 mma8x8 函数进行 8x8 的矩阵乘法累积。
如果没有到达最后一块数据：
- 将寄存器数据存储到共享内存：
  - store_reg_to_smem_tile_transpose 将 ldg_a_reg 的数据转置后存储到共享内存 smemA[write_stage_idx] 中。
  - store_reg_to_smem_tile 将 ldg_b_reg 的数据存储到共享内存 smemB[write_stage_idx] 中。
- 同步线程：确保所有线程完成对共享内存的写入。
- 切换双缓冲区：write_stage_idx ^= 1。
加载下一次迭代的第一块数据：
- 从共享内存加载数据到寄存器：从共享内存 smemA[load_stage_idx ^ 1] 和 smemB[load_stage_idx ^ 1] 加载数据到 a_reg[0] 和 b_reg[0]。
计算最后一块数据：调用 mma8x8 函数进行最后一块数据的矩阵乘法累积。

存储结果

将计算结果存储到全局内存：store_c 函数将寄存器 c 中的计算结果存储到全局内存 C 中。

这段代码通过使用共享内存和寄存器进行双缓冲数据传输，实现了高效的矩阵乘法计算。这样可以在一次迭代中完成数据的加载、计算和存储操作，有效地提高了计算效率。

此外，还可以利用 CUDA 9 的warp-level指令以及Tensor Core进行 GEMM 的优化：

利用Tensor Core进行GEMM优化

__global__ void tensorCoreMatrixMul(float* A, float* B, float* C, int M, int N, int K) {
#if __CUDA_ARCH__ >= 700
    // 适用于 Tensor Cores 的数据类型必须是 half
    half* A_half = reinterpret_cast<half*>(A);
    half* B_half = reinterpret_cast<half*>(B);
    half* C_half = reinterpret_cast<half*>(C);

    int warpM = threadIdx.y / 8;
    int warpN = threadIdx.x / 8;
    int laneM = threadIdx.y % 8;
    int laneN = threadIdx.x % 8;

    wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> a_frag;
    wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::col_major> b_frag;
    wmma::fragment<wmma::accumulator, 16, 16, 16, float> c_frag;

    wmma::fill_fragment(c_frag, 0.0f);

    for (int i = 0; i < K; i += 16) {
        int aRow = warpM * 16;
        int bCol = warpN * 16;

        wmma::load_matrix_sync(a_frag, A_half + aRow * K + i, K);
        wmma::load_matrix_sync(b_frag, B_half + i * N + bCol, N);

        wmma::mma_sync(c_frag, a_frag, b_frag, c_frag);
    }

    int cRow = warpM * 16;
    int cCol = warpN * 16;

    wmma::store_matrix_sync(C_half + cRow * N + cCol, c_frag, N, wmma::mem_row_major);
#endif
}

文章开头问题答案：

直接计算即可；
A_shared和B_shared访问shared memory都不会导致bank conflicts：A_shared会触发广播机制，而B_shared则实现了连续访问。

[!IMPORTANT]
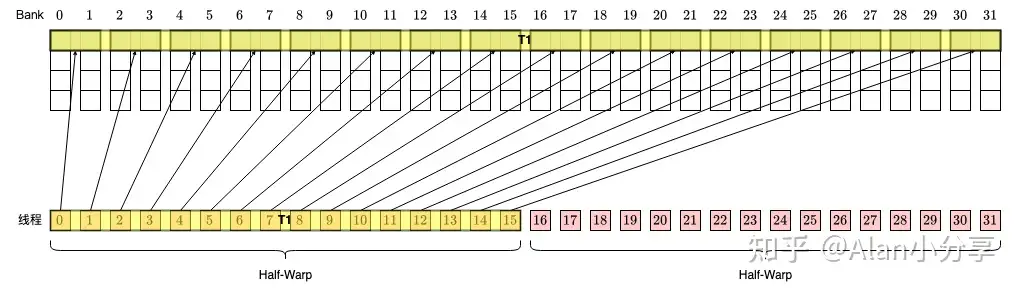
注意这里很难理解的一点，在(double)float32类型中，实际上是将16 个threads 作为half warp的。也就是说每一行32 个bank对应的就是16 个线程，此时对应矩阵乘来说，temp += A_shared[threadIdx.y][k] * B_shared[k][threadIdx.x]; 每次k 的迭代中对于A_shared共享内存都进行了广播，而对于B_shared共享内存则是连续访问，都没有bank conflict.

REFERENCE:THANKS FOR

1. 搞懂 CUDA Shared Memory 上的 bank conflicts 和向量化指令（LDS.128 / float4）的访存特点

2. 矩阵乘法的 CUDA 实现、优化及性能分析

3. CUDA 矩阵乘法终极优化指南