Pre-Norm&Post-Norm

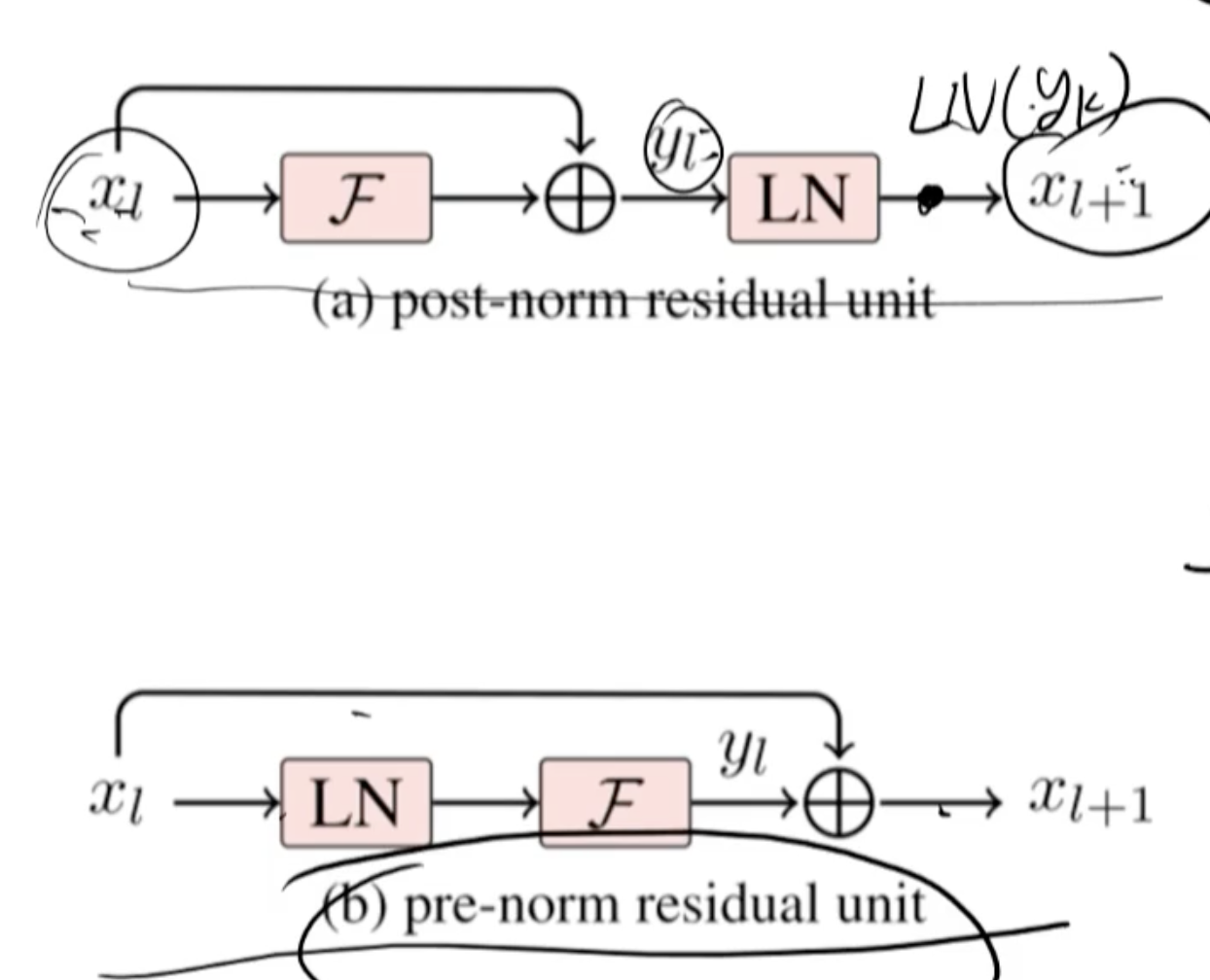
从图中可以看出，两种不同的Transformer结构：Post-Norm Residual Unit 和 Pre-Norm Residual Unit。为了用公式解释它们的优缺点，我们需要先定义一些符号和公式，然后分析每种结构的计算和影响。

定义符号

• ( x_l )：第 ( l ) 层的输入
• ( \mathcal{F}(x_l) )：子层操作（如多头自注意力或前馈网络）
• ( \text{LN}(y_l) )：Layer Normalization 操作
• ( y_l )：子层操作后的输出，即 ( y_l = \mathcal{F}(x_l) )
• ( \tilde{x}_{l+1} )：Post-Norm结构中第 ( l+1 ) 层的输入
• ( x_{l+1} )：Pre-Norm结构中第 ( l+1 ) 层的输入

Post-Norm 结构

在Post-Norm结构中，Layer Normalization在子层操作之后：

[ y_l = \mathcal{F}(x_l) ]
[ \tilde{x}_{l+1} = \text{LN}(x_l + y_l) ]

优点：

1. 初期收敛较快：在训练初期，这种结构能更快地降低损失函数，因为在进行归一化之前，已经经过了子层操作，残差连接使得梯度直接作用于子层输出。
2. 简便实现：这种结构与最初的Transformer论文一致，实现相对简单。

缺点：

1. 梯度不稳定：在深层网络中，梯度容易出现爆炸或消失的现象，尤其是当网络层数增加时，这种不稳定性会更明显。
2. 训练深层模型困难：由于梯度不稳定，训练深层模型可能会出现困难，导致收敛速度减慢或无法收敛。

Pre-Norm 结构

在Pre-Norm结构中，Layer Normalization在子层操作之前：

[ \tilde{x}{l} = \text{LN}(x_l) ]
[ y_l = \mathcal{F}(\tilde{x}{l}) ]
[ x_{l+1} = x_l + y_l ]

优点：

1. 训练稳定性：这种结构能够在训练过程中保持梯度的稳定性，防止梯度爆炸或消失，有助于深层网络的训练。
2. 更适合深层网络：对于深层模型，这种结构能够更好地保持梯度的传递，提升模型的收敛效果。

缺点：

1. 初期训练较慢：在训练初期，这种结构可能需要更多的训练步骤才能达到较好的收敛速度，因为Layer Normalization在子层操作之前，梯度的更新直接受到归一化的影响。
2. 实现复杂度稍高：与Post-Norm结构相比，这种结构稍微复杂一些，但并不显著。

数学公式对比

Post-Norm 计算：

[
\tilde{x}_{l+1} = \text{LN}(x_l + \mathcal{F}(x_l))
]

Pre-Norm 计算：

[
x_{l+1} = x_l + \mathcal{F}(\text{LN}(x_l))
]

梯度传递分析

在反向传播过程中，梯度的计算受到归一化的位置影响：

• Post-Norm：梯度计算在子层操作之后，可能会导致梯度在前向传播过程中积累，从而在深层网络中出现不稳定。
• Pre-Norm：梯度计算在子层操作之前，通过Layer Normalization使得梯度更为平稳，从而在深层网络中更易保持稳定。

总结

• Post-Norm 结构在初期收敛速度较快，适合浅层网络，但在深层网络中可能会出现梯度不稳定的问题。
• Pre-Norm 结构在深层网络中更稳定，适合训练深层模型，但在初期收敛速度可能较慢。

选择使用哪种结构取决于具体的应用场景和网络深度。对于深层网络，Pre-Norm可能是更好的选择，而对于相对浅层的网络，Post-Norm可能更加简便和有效。

分析公式与梯度爆炸和消失

根据图中的公式，我们来看一下Post-Norm和Pre-Norm Residual Unit中梯度的递推公式，并解释为什么Post-Norm更容易导致梯度爆炸和消失。

Post-Norm Residual Unit 的梯度递推公式

首先，我们从Post-Norm Residual Unit的结构入手：
[ \tilde{x}_{l+1} = \text{LN}(x_l + \mathcal{F}(x_l)) ]

对于Post-Norm结构，梯度的反向传播公式如下：
[ \frac{\partial \mathcal{E}}{\partial x_l} = \frac{\partial \mathcal{E}}{\partial \tilde{x}{l+1}} \times \frac{\partial \text{LN}(y_l)}{\partial y_l} \times \prod{k=l}^{L-1} \left( 1 + \frac{\partial \mathcal{F}(x_k, \theta_k)}{\partial x_k} \right) ]

其中，( y_l = x_l + \mathcal{F}(x_l) )，并且(\tilde{x}_{l+1} = \text{LN}(y_l))。

Pre-Norm Residual Unit 的梯度递推公式

接着我们来看Pre-Norm Residual Unit的结构：
[ x_{l+1} = x_l + \mathcal{F}(\text{LN}(x_l)) ]

对于Pre-Norm结构，梯度的反向传播公式如下：
[ \frac{\partial \mathcal{E}}{\partial x_l} = \frac{\partial \mathcal{E}}{\partial x_{l+1}} \times \prod_{k=l}^{L-1} \left( 1 + \frac{\partial \mathcal{F}(\text{LN}(x_k), \theta_k)}{\partial x_k} \right) ]

公式详解与梯度稳定性

• Post-Norm结构中，每一层的梯度计算都包含了(\frac{\partial \text{LN}(y_l)}{\partial y_l})项。Layer Normalization在这里对整体梯度的影响较小，但由于每层的输出都直接影响下一层的输入，因此任何一层的变化都会通过链式法则累积到所有后续层。这种累积效应容易在深层网络中导致梯度的放大或缩小，从而引发梯度爆炸或梯度消失的问题。

• Pre-Norm结构中，Layer Normalization直接作用在每一层的输入上（(\text{LN}(x_l))），这使得每层的输入在进入子层操作之前已经被标准化。这种预处理有助于在反向传播过程中保持梯度的平稳，不容易出现梯度爆炸或消失的情况。

数学解释梯度爆炸和消失

对于Post-Norm结构，如果网络较深，链式法则累积的梯度如下：
[ \frac{\partial \mathcal{E}}{\partial x_l} = \frac{\partial \mathcal{E}}{\partial \tilde{x}{L}} \times \prod{k=l}^{L-1} \left( \frac{\partial \text{LN}(y_k)}{\partial y_k} \times \left(1 + \frac{\partial \mathcal{F}(x_k, \theta_k)}{\partial x_k}\right) \right) ]

由于每层都包含了多个乘积项，任何一个梯度项如果大于1，将导致总体梯度指数级放大（梯度爆炸）；相反，如果梯度项小于1，则会导致总体梯度指数级缩小（梯度消失）。

对于Pre-Norm结构，每层的梯度累积公式为：
[ \frac{\partial \mathcal{E}}{\partial x_l} = \frac{\partial \mathcal{E}}{\partial x_{L}} \times \prod_{k=l}^{L-1} \left( 1 + \frac{\partial \mathcal{F}(\text{LN}(x_k), \theta_k)}{\partial x_k} \right) ]

因为(\text{LN}(x_k))对每层输入进行归一化，使得输入在一定范围内，这大大减小了梯度爆炸和消失的风险。

结论

通过分析公式可以看出：

• Post-Norm结构由于在梯度计算中累积了多个层次的归一化操作和非线性变换，容易导致梯度爆炸和消失。
• Pre-Norm结构通过在每层之前进行归一化，有效地缓解了梯度在深层网络中的放大和缩小，因而更适合深层网络的训练。

这种数学和理论上的分析解释了为什么在实际应用中，Pre-Norm结构在深层网络中更稳定和有效。